# Grab the libraries we want to use
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Clear out pesky warnings
import warnings
warnings.filterwarnings('ignore')
# Set style for better visibility
plt.style.use('ggplot')
# Set random seed for reproducibility
np.random.seed(42)Statistics for Machine Learning
Essential Concepts with Python
Setup
Libraries loaded successfully!
NumPy version: 2.3.4
Pandas version: 2.3.3You can update the style to your liking by looking at this matplotlib style guide.
Introduction
Key Topics
- Exploratory Data Analysis
- Data & Sampling Distributions
- Statistical Inference
- Practical Applications
Why This Matters
- Data science merges statistics, CS, and domain knowledge
- Understanding variability is crucial
- Modern tools enable practical analysis
Chapter 1: Exploratory Data Analysis
Data Types
Numeric Data
- Continuous: Any value
25.2, 24, 29.131414- Useful for precise measurements and calculations
- Discrete: Integer values
25, 24, 29- Useful for counts
Categorical Data
- Categorical: Fixed set of values
'Dog', 'Cat', 'Bat'- typical for factors/ bins / categories
- Binary: Two categories
0, 1orTrue, False- Useful for indicators
- Ordinal: Ordered categories
'low', 'medium', 'high'- categories more similar to neighbor categories
Data Types in Python
Since this is a small dataset, we can display the entire thing:
age visits category is_member rating
0 25 3 A True low
1 30 5 B False medium
2 35 2 A True high
3 40 7 C True medium
If this was a larger dataset, use `df.head()` to see the first couple of entries
We can also see the data type for each feature (column) using `df.dtypes`:
age int64
visits int64
category object
is_member bool
rating object
dtype: objectTabular Data Structure
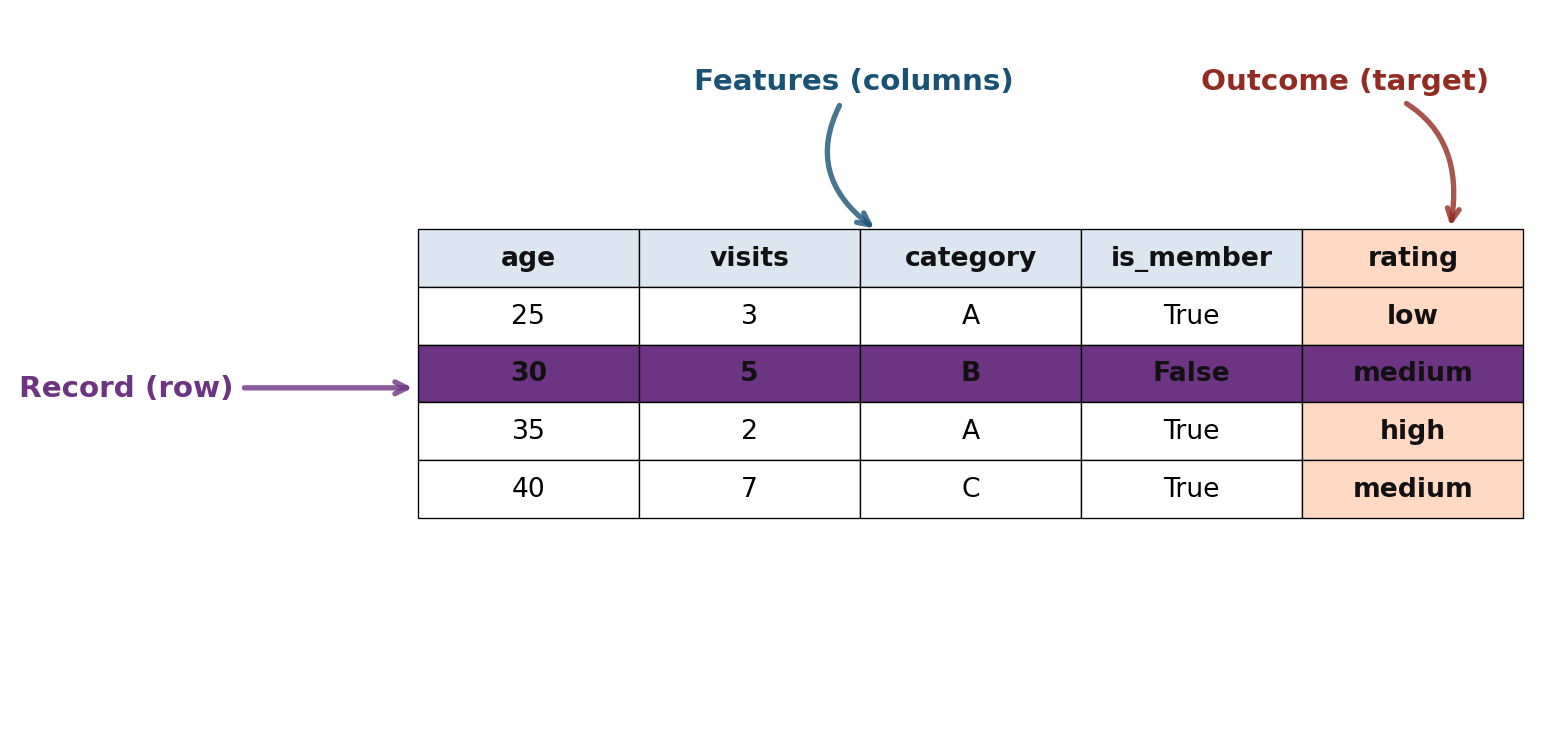
Key Terms
- Data Frame: Basic structure for analysis
- Feature: A column (attribute, predictor, variable)
- Record: A row (case, observation, sample)
- Outcome: Target variable to predict
Estimates of Location
Mean: Average value which is sensitive to outliers (extreme values) \[ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \]
Median: Middle value (50th percentile) which is more robust to outliers \[ \text{Median} = \begin{cases} x_{\frac{n+1}{2}}, & n \text{ odd} \\[2mm] \frac{x_{\frac{n}{2}} + x_{\frac{n}{2}+1}}{2}, & n \text{ even} \end{cases} \]
Trimmed Mean: Average after removing extremes
\[ \bar{x}_{\text{trim}} = \frac{1}{n - 2k} \sum_{i=k+1}^{n-k} x_{(i)} \] where (k) values are removed from each end.
Computing Location Estimates
# Sample data: state populations (in millions)
population = np.array([4.78, 0.71, 6.39, 2.92, 37.25,
5.03, 3.57, 0.90])
mean_pop = np.mean(population)
median_pop = np.median(population)
def trim_mean(data, trim_percent):
n = len(data)
k = int(n * trim_percent)
sorted_data = np.sort(data)
return np.mean(sorted_data[k:n-k])
trimmed_mean = trim_mean(population, 0.1) #trimming 10%
Population data: [ 4.78 0.71 6.39 2.92 37.25 5.03 3.57 0.9 ]
Mean: 7.69M
Median: 4.17M
Trimmed Mean (10%): 7.69M
Note: Mean > Trimmed Mean > Median due to outliersWeighted Mean
# Murder rates and populations by state
murder_rate = np.array([5.7, 5.6, 4.7, 5.6, 4.4])
population = np.array([4.78, 0.71, 6.39, 2.92, 37.25])
states = ['AL', 'AK', 'AZ', 'AR', 'CA']
# Simple mean (treats all states equally)
simple_mean = np.mean(murder_rate)
# Weighted mean (accounts for population)
weighted_mean = np.average(murder_rate, weights=population)
State Data:
AL: Rate=5.7, Pop=4.78M
AK: Rate=5.6, Pop=0.71M
AZ: Rate=4.7, Pop=6.39M
AR: Rate=5.6, Pop=2.92M
CA: Rate=4.4, Pop=37.25M
Simple Mean Murder Rate: 5.20
Weighted Mean Murder Rate: 4.64
Weighted mean is lower because CA (largest state) has lowest rateEstimates of Variability
Range: Difference between maximum and minimum
\[ \text{Range} = x_{\text{max}} - x_{\text{min}} \]Interquartile Range (IQR): Difference between 75th and 25th percentile
\[ \text{IQR} = Q_3 - Q_1 \]Variance: Average squared deviation from mean
\[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]Standard Deviation: Square root of variance
Mean Absolute Deviation (MAD): Average absolute deviation
\[ \text{MAD} = \frac{1}{n} \sum_{i=1}^{n} \big| x_i - \bar{x} \big| \]
Computing Variability
Data: [ 1 4 4 7 10 15]
Measures of Variability:
Variance: 25.37
Standard Deviation: 5.04
Mean Absolute Deviation: 3.83
Range: 14.00
IQR (Q75 - Q25): 5.25Interpreting Variability
So what did all those values even mean?
The numbers in our dataset are spread out, but not too wildly.
The range of 14 tells us how far apart the smallest and largest numbers are.
Looking closer, the middle half of the numbers (the IQR of 6) are much closer together, which means a few unusually high or low numbers are stretching the range.
Measures like variance (36.80) and standard deviation (6.07) give a sense of how much the numbers tend to differ from the average, while the mean absolute deviation (4.83) shows a typical “typical difference” in a way that isn’t affected as much by extreme values.
Altogether, this tells us that while there are a few numbers that are far from the rest, most of the data is relatively clustered near the middle.
Percentiles and Boxplots
Percentiles (5th, 25th, 50th, 75th, 95th):
5th percentile: 0.09
25th percentile: 0.43
50th percentile: 1.25
75th percentile: 2.62
95th percentile: 5.95Show/Hide Code
fig, ax = plt.subplots(figsize=(10, 3))
bp = ax.boxplot(data, vert=False, widths=0.5)
ax.set_xlabel('Value')
ax.set_title('Boxplot of Exponential Distribution')
ax.grid(alpha=0.3)
# Add percentile markers
for p, val in zip([25, 50, 75], [percentiles[1], percentiles[2], percentiles[3]]):
ax.axvline(val, color='red', linestyle='--', alpha=0.5, linewidth=1)
plt.tight_layout()
plt.show()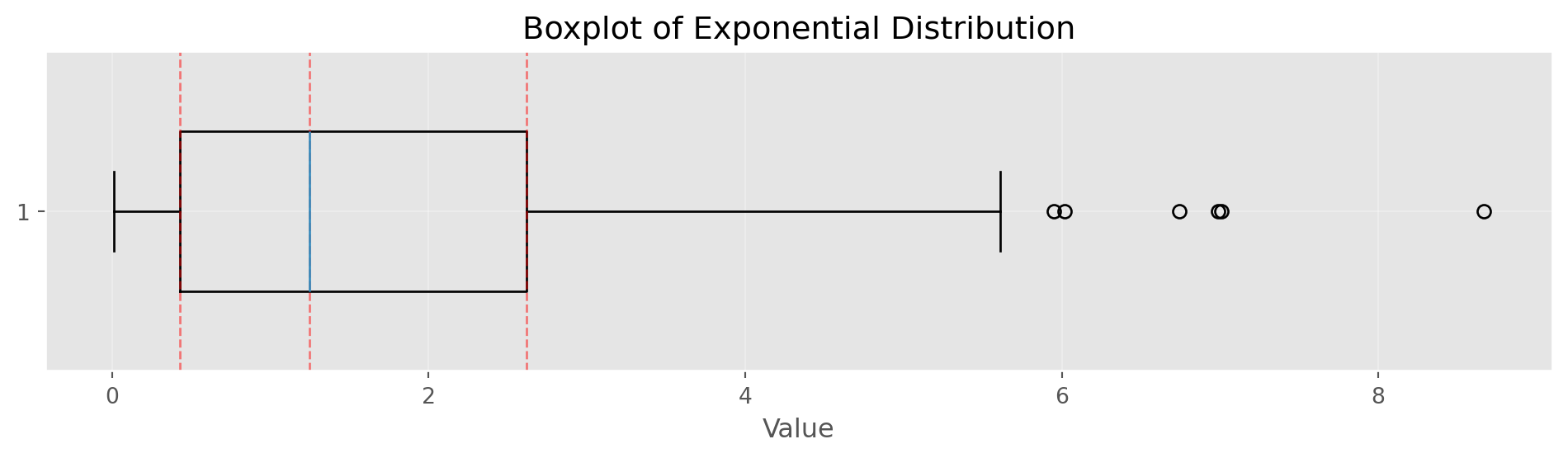
Frequency Tables and Histograms
Show/Hide Code
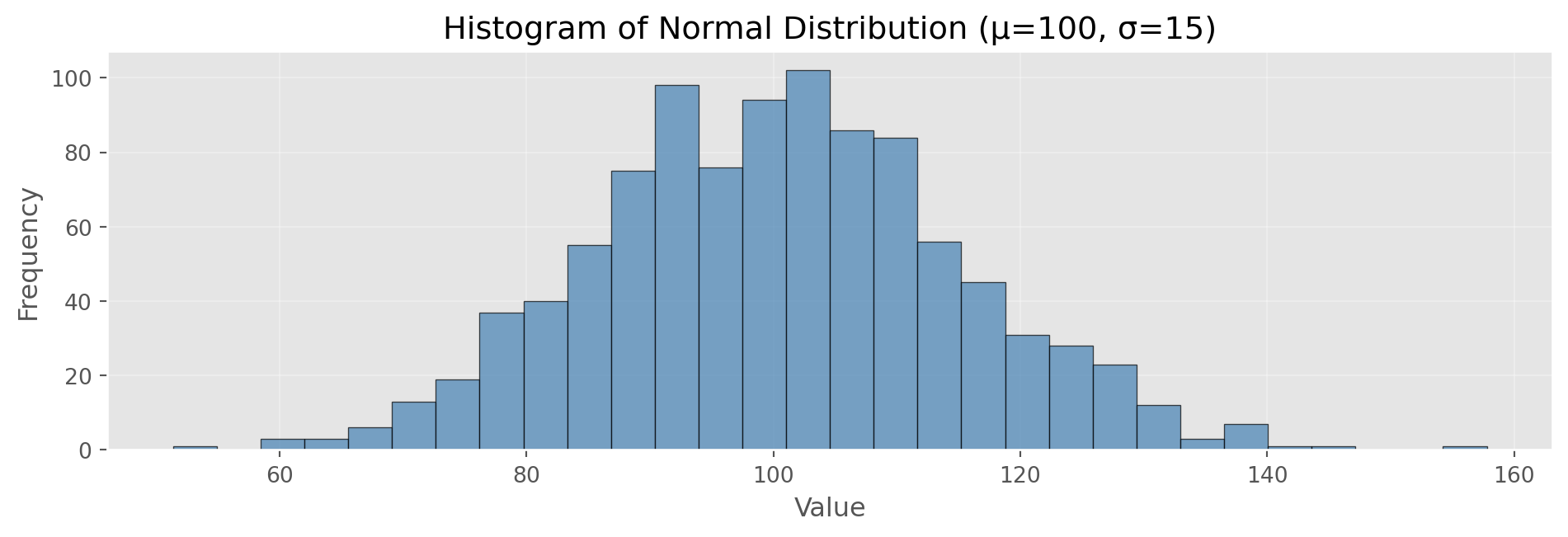
Frequency Table (first 5 bins):
[51.4, 54.9): 1 observations
[54.9, 58.5): 0 observations
[58.5, 62.0): 3 observations
[62.0, 65.6): 3 observations
[65.6, 69.1): 6 observations
Total observations: 1000
Mean: 100.29, Std: 14.69Density Plots
Show/Hide Code
# Kernel density estimation (simple implementation)
def kde(data, x_eval, bandwidth=0.5):
"""Simple Gaussian kernel density estimation"""
n = len(data)
density = np.zeros_like(x_eval, dtype=float)
for xi in data:
kernel = np.exp(-0.5 * ((x_eval - xi) / bandwidth) ** 2)
kernel /= (bandwidth * np.sqrt(2 * np.pi))
density += kernel
return density / n
# Generate data
np.random.seed(42)
data = np.random.normal(100, 15, 1000)
# Generate density estimate
xs = np.linspace(data.min(), data.max(), 200)
density = kde(data, xs, bandwidth=3)
fig, ax = plt.subplots(figsize=(10, 3.5))
ax.hist(data, bins=30, density=True, alpha=0.5,
edgecolor='black', label='Histogram', color='lightblue')
ax.plot(xs, density, 'r-', linewidth=2, label='Density Estimate')
ax.set_xlabel('Value')
ax.set_ylabel('Density')
ax.set_title('Density Plot: Smoothed Distribution')
ax.legend()
ax.grid(alpha=0.3)
plt.tight_layout()
plt.show()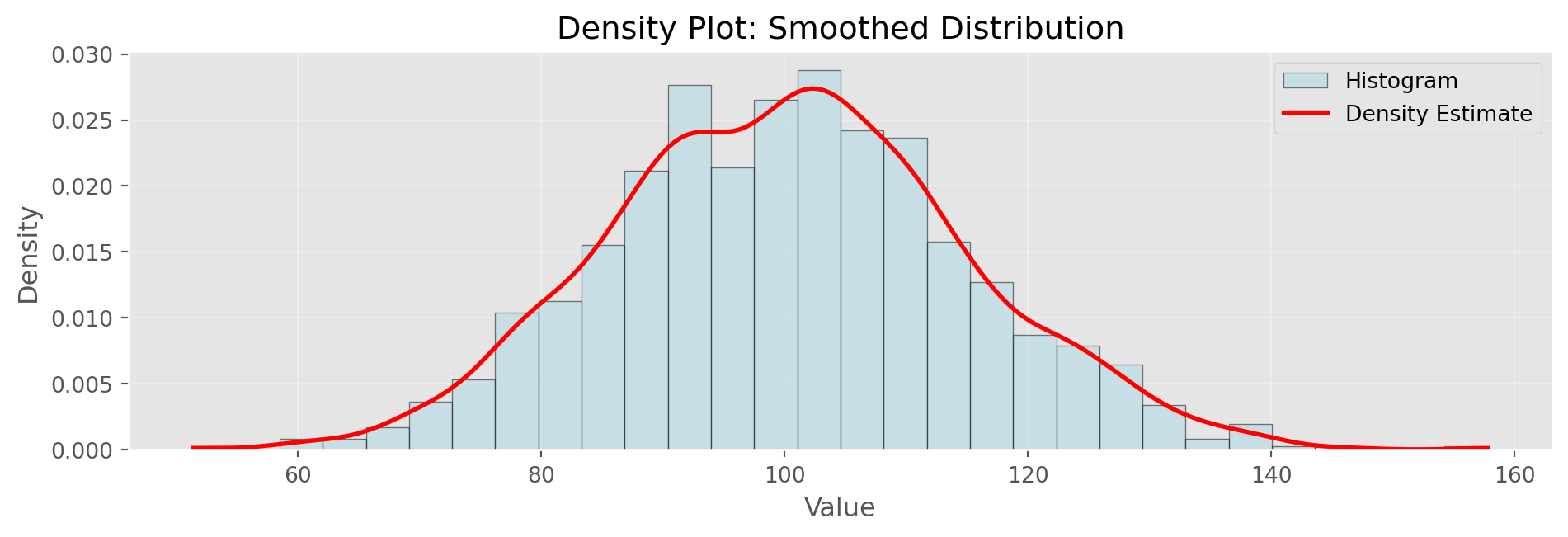
Density estimation smooths the histogram. Bandwidth parameter controls smoothness
Correlation
Pearson Correlation Coefficient
- Measures linear association between variables
- Ranges from -1 (perfect negative) to +1 (perfect positive)
- 0 indicates no linear correlation
\[r = \frac{\sum_{i=1}^{N}(x_i - \bar{x})(y_i - \bar{y})}{(N-1)s_x s_y}\]
Computing Correlation
# Generate correlated data
np.random.seed(42)
x = np.random.normal(0, 1, 100)
y = 2 * x + np.random.normal(0, 0.5, 100)
# Correlation coefficient
correlation = np.corrcoef(x, y)[0, 1]
print(f"Correlation between x and y: {correlation:.3f}")
print(f"Interpretation: Strong positive linear relationship")
# Correlation matrix for multiple variables
z = x + y # Create third variable
data_matrix = np.column_stack([x, y, z])
corr_matrix = np.corrcoef(data_matrix.T)
print("\nCorrelation Matrix:")
print(" x y z")
for i, row in enumerate(corr_matrix):
label = ['x', 'y', 'z'][i]
print(f"{label}: {row[0]:6.3f} {row[1]:6.3f} {row[2]:6.3f}")
print("\nNote: Correlation ranges from -1 (perfect negative) to +1 (perfect positive)")Correlation between x and y: 0.965
Interpretation: Strong positive linear relationship
Correlation Matrix:
x y z
x: 1.000 0.965 0.985
y: 0.965 1.000 0.996
z: 0.985 0.996 1.000
Note: Correlation ranges from -1 (perfect negative) to +1 (perfect positive)Scatterplot with Correlation
np.random.seed(42)
x = np.random.normal(0, 1, 100)
y = 2 * x + np.random.normal(0, 0.5, 100)
correlation = np.corrcoef(x, y)[0, 1]
fig, ax = plt.subplots(figsize=(8, 3.5))
ax.scatter(x, y, alpha=0.6, s=50, color='steelblue', edgecolors='black', linewidth=0.5)
ax.set_xlabel('X', fontsize=12)
ax.set_ylabel('Y', fontsize=12)
ax.set_title(f'Scatterplot with Correlation (r = {correlation:.3f})', fontsize=14)
ax.grid(alpha=0.3)
# Add regression line
z = np.polyfit(x, y, 1)
p = np.poly1d(z)
x_line = np.linspace(x.min(), x.max(), 100)
ax.plot(x_line, p(x_line), "r-", linewidth=2, alpha=0.8, label='Best Fit Line')
ax.legend()
plt.tight_layout()
plt.show()
print(f"Slope of regression line: {z[0]:.3f}")
print(f"Intercept: {z[1]:.3f}")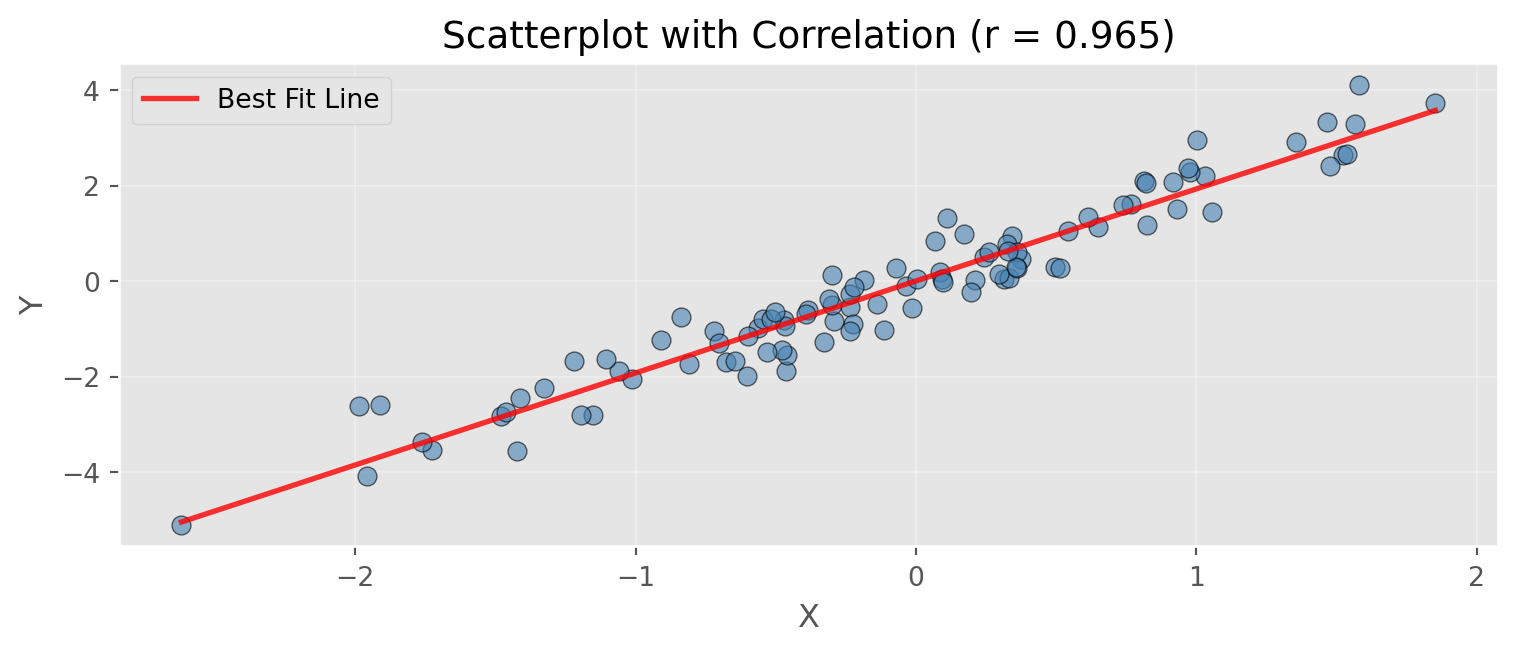
Slope of regression line: 1.928
Intercept: 0.004Hexagonal Binning
# Large dataset example
np.random.seed(42)
n = 10000
x = np.random.normal(0, 1, n)
y = 2 * x + np.random.normal(0, 1, n)
fig, ax = plt.subplots(figsize=(10, 3.5))
hb = ax.hexbin(x, y, gridsize=30, cmap='Blues', mincnt=1, edgecolors='black', linewidths=0.2)
cb = plt.colorbar(hb, ax=ax, label='Count')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_title(f'Hexagonal Binning for Large Datasets (n={n:,})')
ax.grid(alpha=0.3)
plt.tight_layout()
plt.show()
print(f"Total data points: {n:,}")
print(f"Correlation: {np.corrcoef(x, y)[0,1]:.3f}")
print(f"\nHexagonal binning aggregates dense point clouds into bins")
print(f"Useful when scatterplots become too dense to interpret")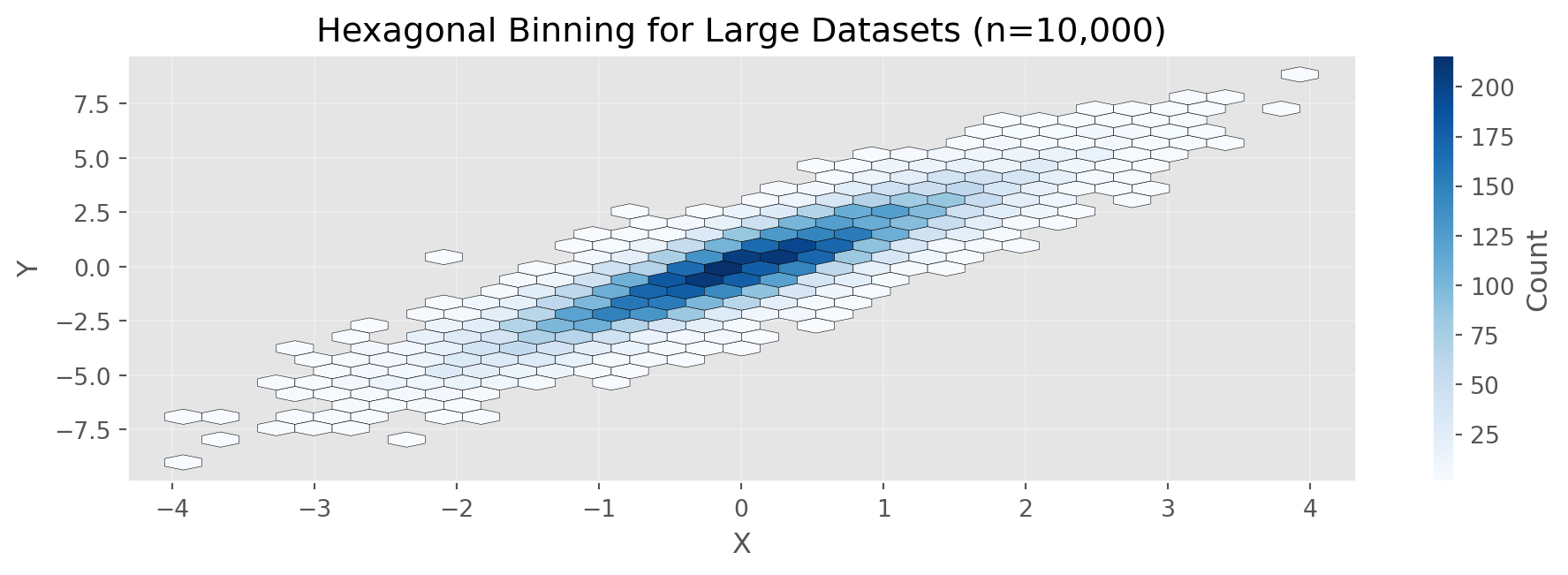
Total data points: 10,000
Correlation: 0.894
Hexagonal binning aggregates dense point clouds into bins
Useful when scatterplots become too dense to interpretCategorical Data: Bar Charts
# Flight delay causes
causes = ['Carrier', 'ATC', 'Weather', 'Security', 'Inbound']
percentages = [23.02, 30.40, 4.03, 0.12, 42.43]
fig, ax = plt.subplots(figsize=(10, 3.5))
bars = ax.bar(causes, percentages, color='steelblue', edgecolor='black', alpha=0.8)
ax.set_ylabel('Percentage (%)', fontsize=12)
ax.set_title('Airline Delays by Cause at DFW Airport', fontsize=14)
ax.grid(axis='y', alpha=0.3)
# Add percentage labels on bars
for bar, pct in zip(bars, percentages):
height = bar.get_height()
ax.text(bar.get_x() + bar.get_width()/2., height,
f'{pct:.1f}%', ha='center', va='bottom', fontsize=10)
plt.tight_layout()
plt.show()
print("Delay Causes Summary:")
for cause, pct in zip(causes, percentages):
print(f" {cause:12s}: {pct:5.2f}%")
print(f"\nTotal: {sum(percentages):.2f}%")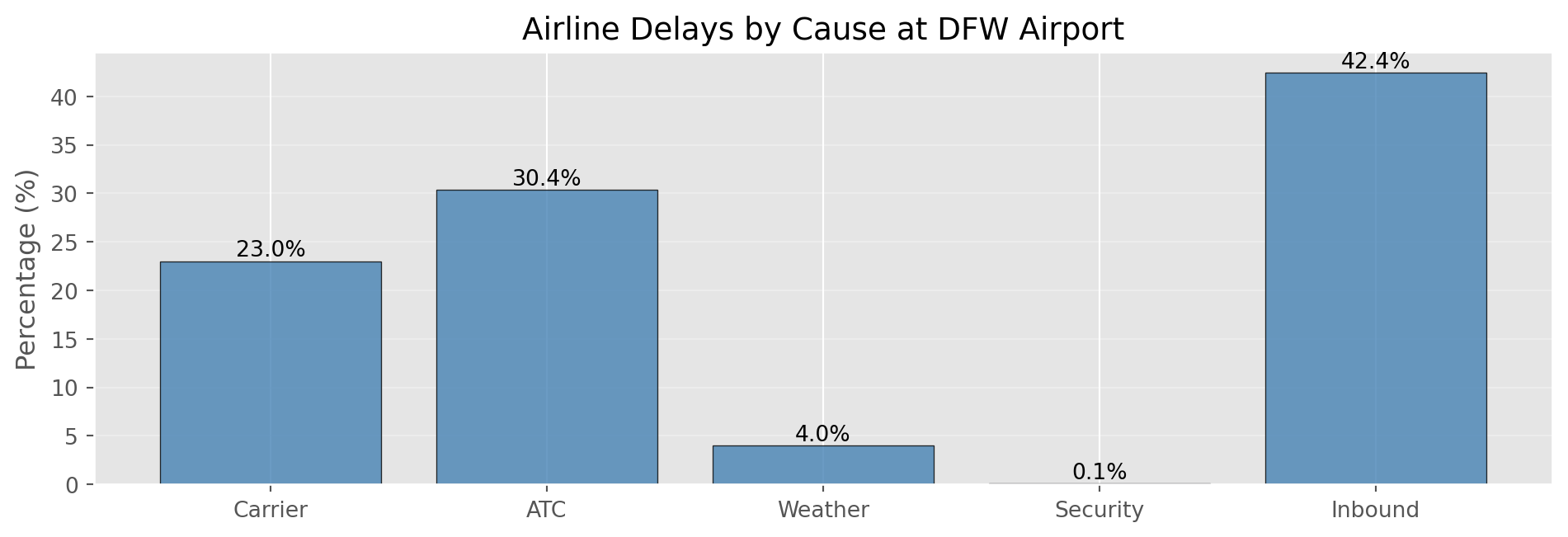
Delay Causes Summary:
Carrier : 23.02%
ATC : 30.40%
Weather : 4.03%
Security : 0.12%
Inbound : 42.43%
Total: 100.00%Contingency Tables
# Create sample loan data
np.random.seed(42)
grades = np.random.choice(['A', 'B', 'C', 'D'], size=1000,
p=[0.2, 0.3, 0.3, 0.2])
status = np.random.choice(['Paid', 'Current', 'Late', 'Charged Off'],
size=1000, p=[0.25, 0.65, 0.05, 0.05])
# Create contingency table
ct = pd.crosstab(grades, status, margins=True)
print("Contingency Table (Counts):")
print(ct)
# With row percentages
ct_pct = pd.crosstab(grades, status, normalize='index') * 100
print("\n\nRow Percentages (by Grade):")
print(ct_pct.round(1))
print("\n\nInterpretation:")
print("Each cell shows percentage of loans in that grade with that status")
print("Example: What % of Grade A loans are Current, Paid, Late, etc.?")Contingency Table (Counts):
col_0 Charged Off Current Late Paid All
row_0
A 12 143 9 61 225
B 14 174 14 76 278
C 20 196 10 72 298
D 13 132 5 49 199
All 59 645 38 258 1000
Row Percentages (by Grade):
col_0 Charged Off Current Late Paid
row_0
A 5.3 63.6 4.0 27.1
B 5.0 62.6 5.0 27.3
C 6.7 65.8 3.4 24.2
D 6.5 66.3 2.5 24.6
Interpretation:
Each cell shows percentage of loans in that grade with that status
Example: What % of Grade A loans are Current, Paid, Late, etc.?Violin Plots
# Compare distributions across groups
np.random.seed(42)
group_a = np.random.normal(10, 2, 100)
group_b = np.random.normal(12, 3, 100)
group_c = np.random.normal(11, 1.5, 100)
data_violin = [group_a, group_b, group_c]
fig, ax = plt.subplots(figsize=(10, 3.5))
parts = ax.violinplot(data_violin, positions=[1, 2, 3],
showmeans=True, showmedians=True)
ax.set_xticks([1, 2, 3])
ax.set_xticklabels(['Group A', 'Group B', 'Group C'])
ax.set_ylabel('Value', fontsize=12)
ax.set_title('Violin Plot: Comparing Distribution Shapes', fontsize=14)
ax.grid(alpha=0.3, axis='y')
plt.tight_layout()
plt.show()
print("Summary Statistics by Group:")
for name, data in [('A', group_a), ('B', group_b), ('C', group_c)]:
print(f" Group {name}: Mean={np.mean(data):.2f}, Std={np.std(data, ddof=1):.2f}")
print("\nViolin width shows density at each value level")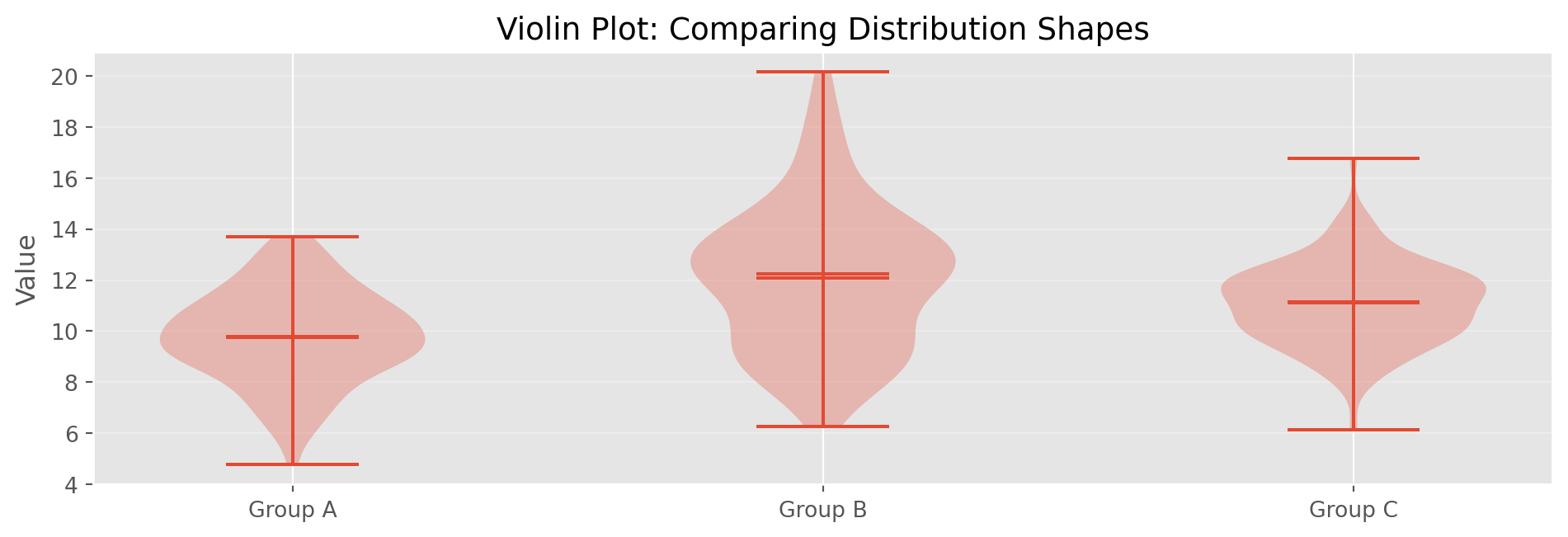
Summary Statistics by Group:
Group A: Mean=9.79, Std=1.82
Group B: Mean=12.07, Std=2.86
Group C: Mean=11.10, Std=1.63
Violin width shows density at each value levelChapter 2: Data and Sampling Distributions
Random Sampling Concepts
Key Terms
- Population: The complete dataset (real or theoretical)
- Sample: A subset drawn from the population
- Random Sampling: Each element has equal chance of selection
- Sample Bias: Sample systematically differs from population
- Stratified Sampling: Random sampling from defined subgroups
Random Sampling in Python
# Create a population
np.random.seed(42)
population = np.random.normal(100, 15, 10000)
# Simple random sample
sample_size = 100
simple_sample = np.random.choice(population, size=sample_size,
replace=False)
print(f"Population size: {len(population):,}")
print(f"Sample size: {sample_size}")
print(f"\nPopulation Mean: {np.mean(population):.2f}")
print(f"Population Std Dev: {np.std(population, ddof=1):.2f}")
print(f"\nSample Mean: {np.mean(simple_sample):.2f}")
print(f"Sample Std Dev: {np.std(simple_sample, ddof=1):.2f}")
# Show difference
diff = abs(np.mean(simple_sample) - np.mean(population))
print(f"\nDifference in means: {diff:.2f}")
print(f"Sampling error (expected): ~{15/np.sqrt(sample_size):.2f}")Population size: 10,000
Sample size: 100
Population Mean: 99.97
Population Std Dev: 15.05
Sample Mean: 101.75
Sample Std Dev: 16.06
Difference in means: 1.78
Sampling error (expected): ~1.50Stratified Sampling
# Create stratified population (3 distinct groups)
np.random.seed(42)
stratum_a = np.random.normal(100, 10, 7000) # 70% of population
stratum_b = np.random.normal(120, 15, 2000) # 20% of population
stratum_c = np.random.normal(90, 12, 1000) # 10% of population
full_population = np.concatenate([stratum_a, stratum_b, stratum_c])
true_mean = np.mean(full_population)
# Sample from each stratum proportionally
n = 300
sample_a = np.random.choice(stratum_a, size=int(n*0.7))
sample_b = np.random.choice(stratum_b, size=int(n*0.2))
sample_c = np.random.choice(stratum_c, size=int(n*0.1))
stratified_sample = np.concatenate([sample_a, sample_b, sample_c])
# Compare with simple random sample
simple_sample = np.random.choice(full_population, size=n)
print(f"True Population Mean: {true_mean:.2f}")
print(f"Stratified Sample Mean: {np.mean(stratified_sample):.2f}")
print(f"Simple Random Sample Mean: {np.mean(simple_sample):.2f}")
print(f"\nStratified sampling ensures representation from all groups")True Population Mean: 103.00
Stratified Sample Mean: 102.56
Simple Random Sample Mean: 101.53
Stratified sampling ensures representation from all groupsSampling Distribution
The sampling distribution is the distribution of a sample statistic over many samples.
Key Insight: Even if individual data isn’t normally distributed, sample means tend toward normality (Central Limit Theorem)
Demonstrating Sampling Distribution
# Draw many samples and compute means
np.random.seed(42)
population = np.random.exponential(scale=2, size=10000)
sample_means = [np.mean(np.random.choice(population, 30))
for _ in range(1000)]
fig, axes = plt.subplots(1, 2, figsize=(12, 3.5))
axes[0].hist(population, bins=50, edgecolor='black', alpha=0.7, color='lightcoral')
axes[0].set_title('Population Distribution (Exponential)', fontsize=12)
axes[0].set_xlabel('Value')
axes[0].set_ylabel('Frequency')
axes[1].hist(sample_means, bins=30, edgecolor='black', alpha=0.7, color='lightblue')
axes[1].set_title('Sampling Distribution of Mean (n=30, 1000 samples)', fontsize=12)
axes[1].set_xlabel('Sample Mean')
axes[1].set_ylabel('Frequency')
plt.tight_layout()
plt.show()
print(f"Population mean: {np.mean(population):.3f}")
print(f"Mean of sample means: {np.mean(sample_means):.3f}")
print(f"Std dev of sample means: {np.std(sample_means):.3f}")
print(f"\nNote: Even though population is skewed, sampling distribution is normal!")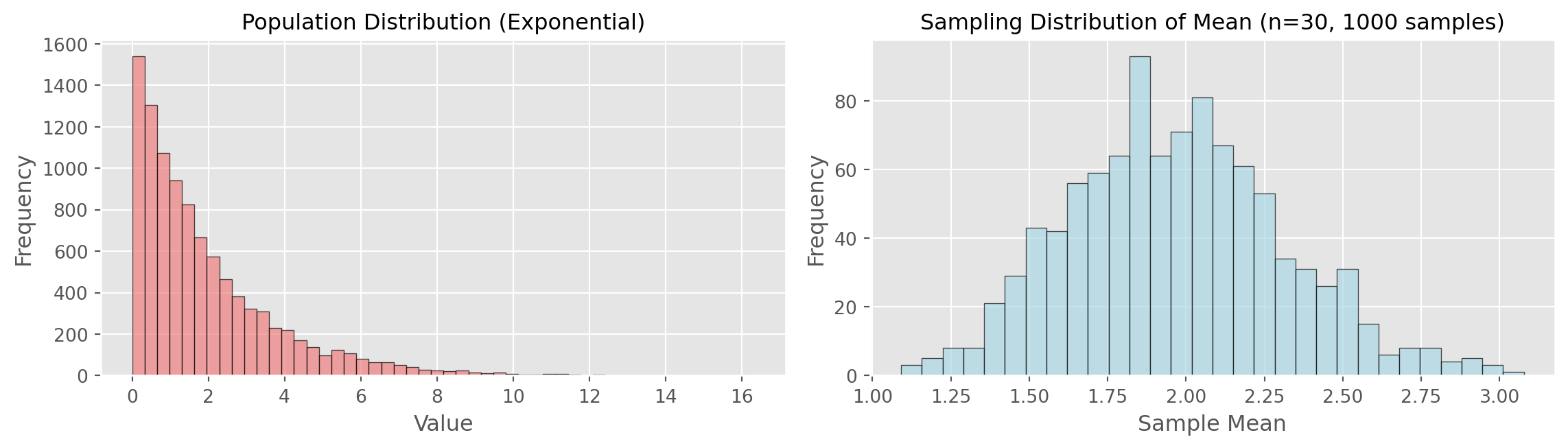
Population mean: 1.955
Mean of sample means: 1.968
Std dev of sample means: 0.343
Note: Even though population is skewed, sampling distribution is normal!Central Limit Theorem
The CLT states: As sample size increases, the sampling distribution of the mean approaches a normal distribution, regardless of the population’s distribution.
Requirements: - Large enough sample size (typically n > 30) - Population not too heavily skewed
Standard Error
Standard Error (SE): The standard deviation of a sampling distribution
\[SE = \frac{s}{\sqrt{n}}\]
Where: - s = sample standard deviation - n = sample size
Square-root of n rule: To reduce SE by half, need 4× the sample size
Computing Standard Error
# Generate sample
np.random.seed(42)
sample = np.random.normal(100, 15, 50)
# Calculate standard error (formula-based)
se_formula = np.std(sample, ddof=1) / np.sqrt(len(sample))
print(f"Sample size: {len(sample)}")
print(f"Sample Mean: {np.mean(sample):.2f}")
print(f"Sample Std Dev: {np.std(sample, ddof=1):.2f}")
print(f"Standard Error (formula): {se_formula:.2f}")
# Verify with multiple samples (empirical approach)
sample_means = [np.mean(np.random.normal(100, 15, 50))
for _ in range(1000)]
empirical_se = np.std(sample_means)
print(f"\nEmpirical SE (from 1000 samples): {empirical_se:.2f}")
print(f"\nThey match! SE = σ / √n = 15 / √50 ≈ {15/np.sqrt(50):.2f}")
# Demonstrate square-root of n rule
print(f"\nSquare-root of n rule:")
print(f" To halve SE, need 4× sample size: {se_formula:.2f} → {se_formula/2:.2f}")
print(f" New sample size needed: {50 * 4} (was 50)")Sample size: 50
Sample Mean: 96.62
Sample Std Dev: 14.01
Standard Error (formula): 1.98
Empirical SE (from 1000 samples): 2.15
They match! SE = σ / √n = 15 / √50 ≈ 2.12
Square-root of n rule:
To halve SE, need 4× sample size: 1.98 → 0.99
New sample size needed: 200 (was 50)The Bootstrap
Bootstrap Resampling: Sample WITH replacement from observed data to estimate sampling distribution
Algorithm: 1. Draw n samples with replacement from original data 2. Calculate statistic of interest 3. Repeat B times (e.g., 1000) 4. Use distribution of statistics for inference
Bootstrap Implementation
# Original sample
np.random.seed(42)
original_sample = np.random.normal(100, 15, 50)
# Bootstrap resampling
n_bootstrap = 1000
bootstrap_means = []
for _ in range(n_bootstrap):
resample = np.random.choice(original_sample,
size=len(original_sample),
replace=True) # WITH replacement!
bootstrap_means.append(np.mean(resample))
bootstrap_means = np.array(bootstrap_means)
# Plot results
fig, ax = plt.subplots(figsize=(10, 3.5))
ax.hist(bootstrap_means, bins=30, edgecolor='black', alpha=0.7, color='lightgreen')
ax.axvline(np.mean(original_sample), color='red',
linestyle='--', linewidth=2, label='Original Sample Mean')
ax.set_xlabel('Bootstrap Mean')
ax.set_ylabel('Frequency')
ax.set_title(f'Bootstrap Distribution ({n_bootstrap} resamples)')
ax.legend()
ax.grid(alpha=0.3)
plt.tight_layout()
plt.show()
print(f"Original Sample Mean: {np.mean(original_sample):.2f}")
print(f"Bootstrap SE: {np.std(bootstrap_means):.2f}")
print(f"Formula SE: {np.std(original_sample, ddof=1)/np.sqrt(50):.2f}")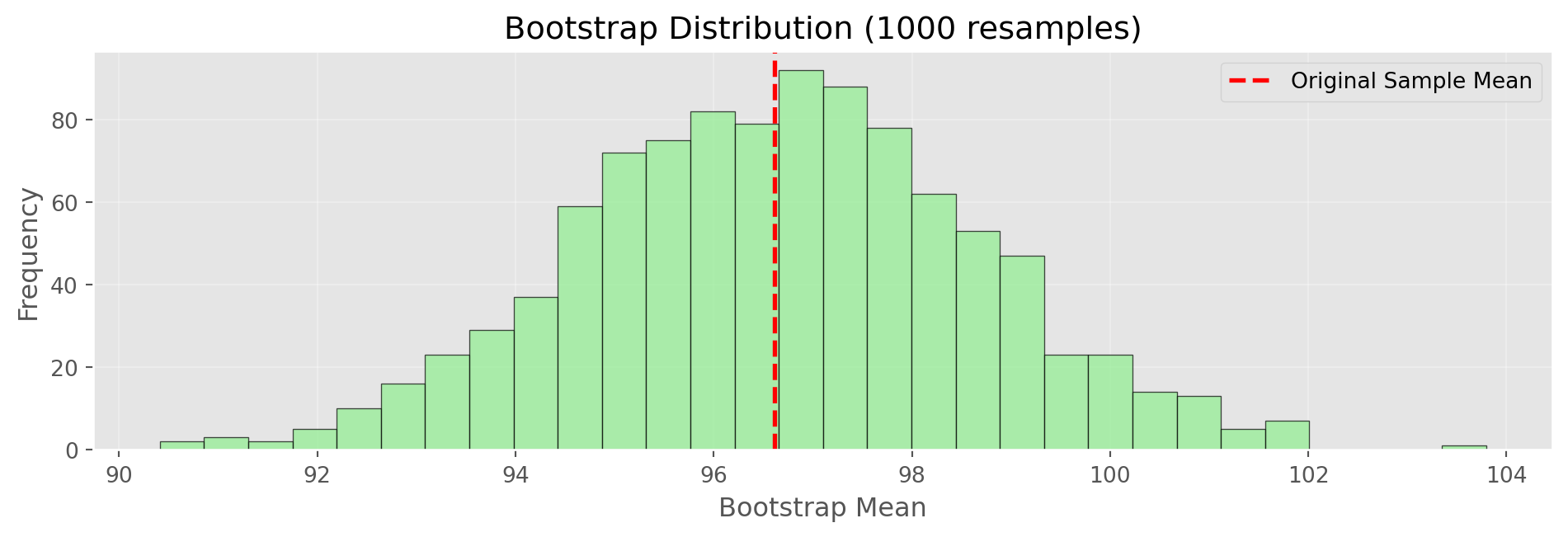
Original Sample Mean: 96.62
Bootstrap SE: 2.00
Formula SE: 1.98Confidence Intervals
Confidence Interval: A range that likely contains the true population parameter
90% CI from Bootstrap: - Take the 5th and 95th percentiles of bootstrap distribution - Interpretation: If we repeated this process many times, 90% of intervals would contain the true parameter
Computing Confidence Intervals
# Use bootstrap distribution from previous slide
np.random.seed(42)
original_sample = np.random.normal(100, 15, 50)
bootstrap_means = [np.mean(np.random.choice(original_sample,
len(original_sample), replace=True))
for _ in range(1000)]
# 90% Confidence interval
ci_90_lower = np.percentile(bootstrap_means, 5)
ci_90_upper = np.percentile(bootstrap_means, 95)
# 95% Confidence interval
ci_95_lower = np.percentile(bootstrap_means, 2.5)
ci_95_upper = np.percentile(bootstrap_means, 97.5)
print(f"Original Sample Mean: {np.mean(original_sample):.2f}")
print(f"\n90% Confidence Interval: ({ci_90_lower:.2f}, {ci_90_upper:.2f})")
print(f" Width: {ci_90_upper - ci_90_lower:.2f}")
print(f"\n95% Confidence Interval: ({ci_95_lower:.2f}, {ci_95_upper:.2f})")
print(f" Width: {ci_95_upper - ci_95_lower:.2f}")
print(f"\nInterpretation:")
print(f"We are 95% confident the true population mean lies between")
print(f"{ci_95_lower:.2f} and {ci_95_upper:.2f}")
print(f"\nNote: Higher confidence → wider interval")Original Sample Mean: 96.62
90% Confidence Interval: (93.43, 99.96)
Width: 6.52
95% Confidence Interval: (92.73, 100.68)
Width: 7.95
Interpretation:
We are 95% confident the true population mean lies between
92.73 and 100.68
Note: Higher confidence → wider intervalNormal Distribution
# Normal PDF function
def normal_pdf(x, mu=0, sigma=1):
"""Calculate normal probability density function"""
return (1 / (sigma * np.sqrt(2 * np.pi))) * \
np.exp(-0.5 * ((x - mu) / sigma) ** 2)
# Generate normal distribution
x = np.linspace(-4, 4, 1000)
y = normal_pdf(x, 0, 1)
fig, ax = plt.subplots(figsize=(10, 3.5))
ax.plot(x, y, 'b-', linewidth=2, label='Standard Normal')
ax.fill_between(x, y, where=(x >= -1) & (x <= 1),
alpha=0.3, label='68% (±1 SD)', color='blue')
ax.fill_between(x, y, where=((x >= -2) & (x < -1)) | ((x > 1) & (x <= 2)),
alpha=0.2, label='95% (±2 SD)', color='green')
ax.set_xlabel('Z-score (Standard Deviations)')
ax.set_ylabel('Density')
ax.set_title('Standard Normal Distribution')
ax.legend()
ax.grid(alpha=0.3)
plt.tight_layout()
plt.show()
print("Standard Normal Properties:")
print(" 68% of data within ±1 SD")
print(" 95% of data within ±2 SD")
print(" 99.7% of data within ±3 SD")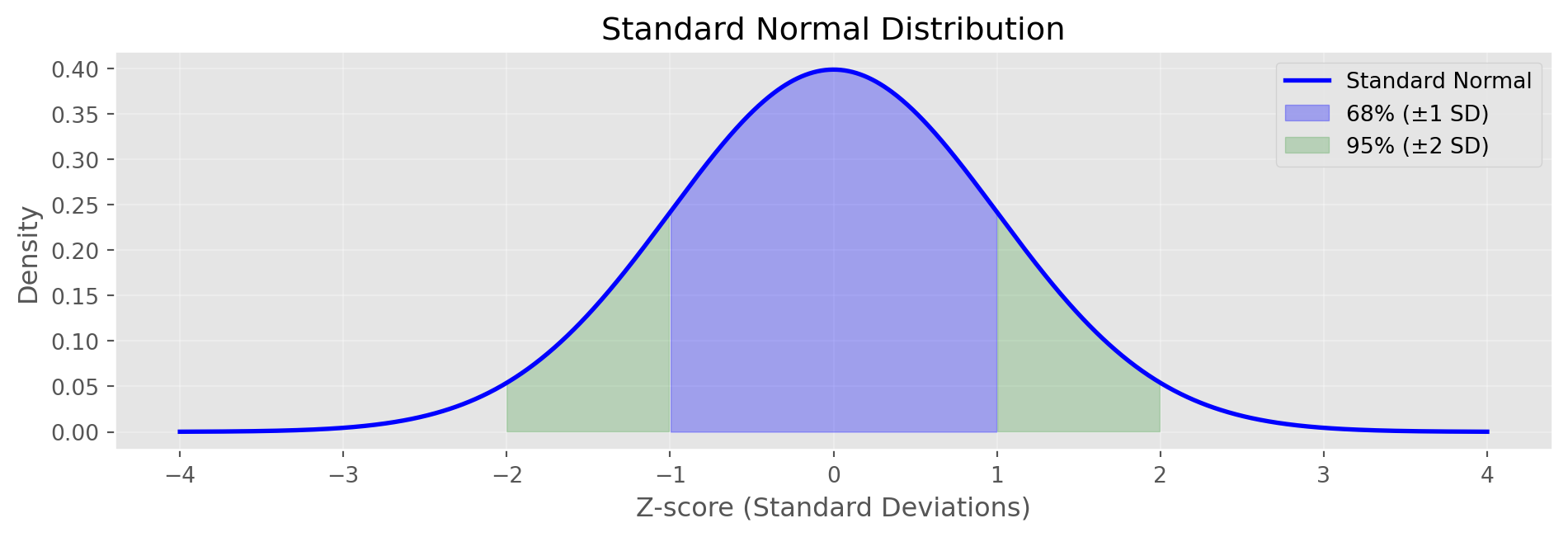
Standard Normal Properties:
68% of data within ±1 SD
95% of data within ±2 SD
99.7% of data within ±3 SDQ-Q Plots
def qq_plot(data, ax, title):
"""Create Q-Q plot manually"""
standardized = (data - np.mean(data)) / np.std(data, ddof=1)
standardized = np.sort(standardized)
n = len(standardized)
theoretical = np.array([np.percentile(np.random.standard_normal(10000),
100 * (i - 0.5) / n) for i in range(1, n + 1)])
ax.scatter(theoretical, standardized, alpha=0.6, s=30)
ax.plot([-3, 3], [-3, 3], 'r--', linewidth=2, label='Perfect Normal')
ax.set_xlabel('Theoretical Quantiles')
ax.set_ylabel('Sample Quantiles')
ax.set_title(title)
ax.grid(alpha=0.3)
ax.legend()
np.random.seed(42)
normal_data = np.random.normal(0, 1, 100)
exp_data = np.random.exponential(1, 100)
fig, axes = plt.subplots(1, 2, figsize=(12, 3.5))
qq_plot(normal_data, axes[0], 'Q-Q Plot: Normal Data')
qq_plot(exp_data, axes[1], 'Q-Q Plot: Exponential Data')
plt.tight_layout()
plt.show()
print("Interpretation:")
print(" Left: Points on line → data is normally distributed")
print(" Right: Points deviate → data is NOT normally distributed")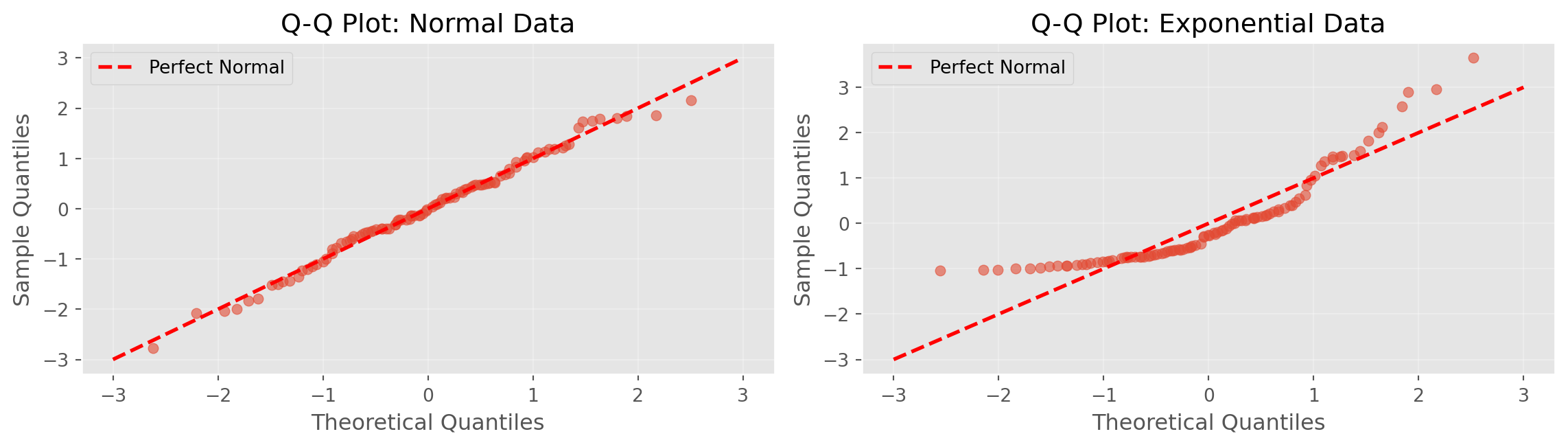
Interpretation:
Left: Points on line → data is normally distributed
Right: Points deviate → data is NOT normally distributedBinomial Distribution
Binomial: Distribution of number of successes in n independent trials
Parameters: - n: number of trials - p: probability of success
Example: 10 coin flips, probability of getting 6 heads
Binomial Distribution in Python
def binomial_pmf(k, n, p):
"""Calculate binomial probability mass function"""
def factorial(x):
if x <= 1: return 1
return x * factorial(x - 1)
def comb(n, k):
return factorial(n) // (factorial(k) * factorial(n - k))
return comb(n, k) * (p ** k) * ((1 - p) ** (n - k))
n = 20 # trials
p = 0.3 # probability of success
x = np.arange(0, n+1)
pmf = np.array([binomial_pmf(k, n, p) for k in x])
fig, ax = plt.subplots(figsize=(10, 3.5))
ax.bar(x, pmf, edgecolor='black', alpha=0.7, color='steelblue')
ax.set_xlabel('Number of Successes')
ax.set_ylabel('Probability')
ax.set_title(f'Binomial Distribution (n={n} trials, p={p} success probability)')
ax.grid(alpha=0.3, axis='y')
plt.tight_layout()
plt.show()
prob_5 = binomial_pmf(5, n, p)
prob_le_5 = sum([binomial_pmf(k, n, p) for k in range(6)])
print(f"P(exactly 5 successes) = {prob_5:.4f}")
print(f"P(5 or fewer successes) = {prob_le_5:.4f}")
print(f"Expected value (mean) = n×p = {n*p:.1f}")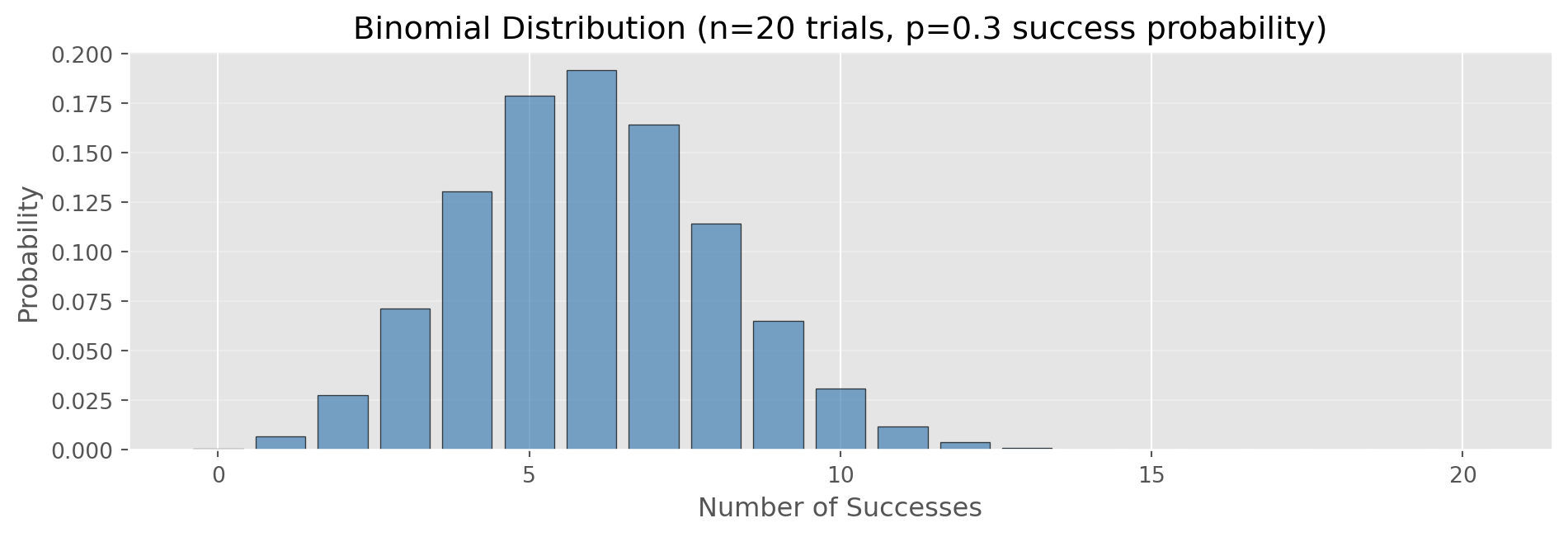
P(exactly 5 successes) = 0.1789
P(5 or fewer successes) = 0.4164
Expected value (mean) = n×p = 6.0Poisson Distribution
Poisson: Distribution of events occurring at a constant rate
Parameter: λ (lambda) = average rate
Examples: - Website visits per hour - Customer calls per minute - Defects per unit
Poisson Distribution in Python
import math
def poisson_pmf(k, lam):
"""Calculate Poisson probability mass function"""
return (lam ** k) * np.exp(-lam) / math.factorial(k)
lambda_rate = 3 # average events per interval
x = np.arange(0, 15)
pmf = np.array([poisson_pmf(k, lambda_rate) for k in x])
fig, ax = plt.subplots(figsize=(10, 3.5))
ax.bar(x, pmf, edgecolor='black', alpha=0.7, color='coral')
ax.set_xlabel('Number of Events')
ax.set_ylabel('Probability')
ax.set_title(f'Poisson Distribution (λ={lambda_rate} events/interval)')
ax.grid(alpha=0.3, axis='y')
plt.tight_layout()
plt.show()
# Generate random Poisson data (simulation)
np.random.seed(42)
poisson_data = np.random.poisson(lambda_rate, 100)
print(f"Theoretical mean (λ): {lambda_rate}")
print(f"Simulated mean: {np.mean(poisson_data):.2f}")
print(f"Theoretical variance (also λ): {lambda_rate}")
print(f"Simulated variance: {np.var(poisson_data, ddof=1):.2f}")
print(f"\nUse for: arrivals, calls, defects per time/space unit")
Theoretical mean (λ): 3
Simulated mean: 2.78
Theoretical variance (also λ): 3
Simulated variance: 3.14
Use for: arrivals, calls, defects per time/space unitExponential Distribution
Exponential: Time between Poisson events
Parameter: λ (rate parameter)
Example: Time between customer arrivals
Exponential Distribution in Python
def exponential_pdf(x, lam):
"""Calculate exponential probability density function"""
return lam * np.exp(-lam * x)
rate = 0.5 # events per unit time
scale = 1/rate # mean time between events
x = np.linspace(0, 10, 1000)
pdf = exponential_pdf(x, rate)
fig, ax = plt.subplots(figsize=(10, 3.5))
ax.plot(x, pdf, 'b-', linewidth=2, label=f'rate={rate}')
ax.fill_between(x, pdf, alpha=0.3)
ax.set_xlabel('Time Between Events')
ax.set_ylabel('Density')
ax.set_title(f'Exponential Distribution (λ={rate}, mean={scale:.1f})')
ax.legend()
ax.grid(alpha=0.3)
plt.tight_layout()
plt.show()
# Generate random exponential data
np.random.seed(42)
exp_data = np.random.exponential(scale=scale, size=100)
print(f"Theoretical mean (1/λ): {scale:.2f}")
print(f"Simulated mean: {np.mean(exp_data):.2f}")
print(f"\nUse for: time between events (complement to Poisson)")
print(f"Example: time between customer arrivals")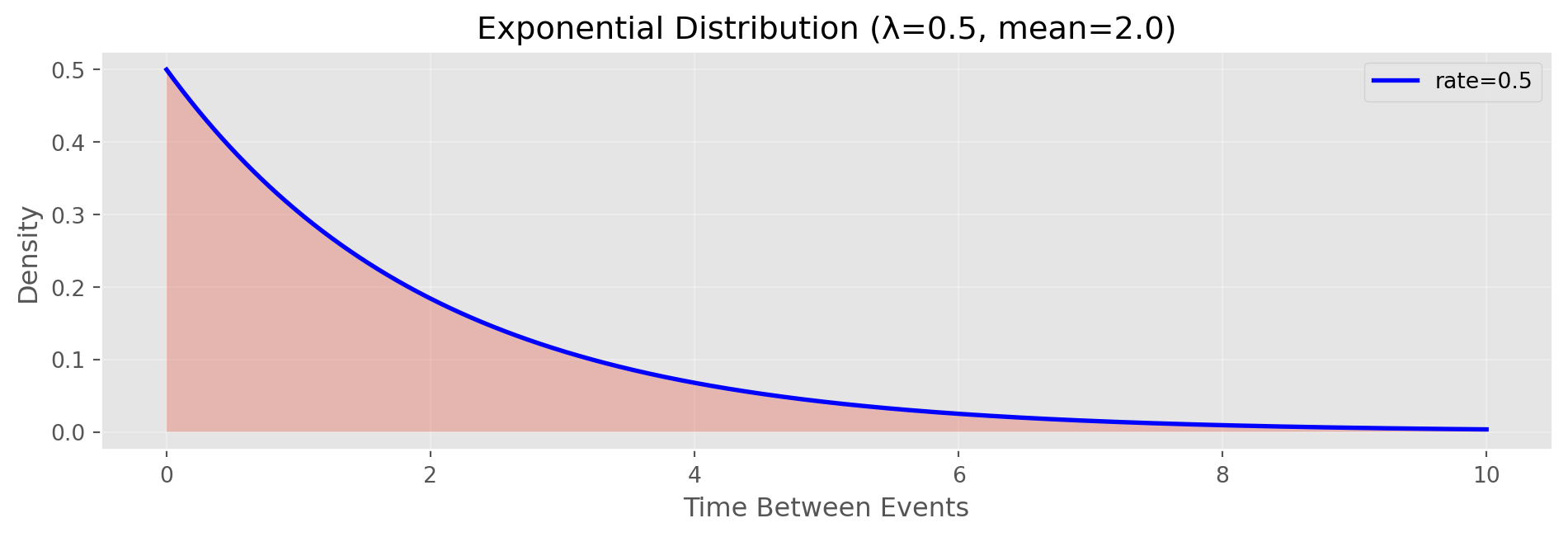
Theoretical mean (1/λ): 2.00
Simulated mean: 1.83
Use for: time between events (complement to Poisson)
Example: time between customer arrivalsKey Takeaways
EDA
- Understand your data types
- Use robust statistics
- Visualize distributions
- Check for outliers
Sampling
- Random sampling reduces bias
- Bootstrap estimates uncertainty
- Confidence intervals quantify precision
- Choose appropriate distributions
Practical Workflow
- Load and inspect data
- Calculate summary statistics (mean, median, std)
- Visualize distributions (histograms, boxplots)
- Check for outliers and anomalies
- Assess relationships (correlation, scatterplots)
- Estimate uncertainty (bootstrap, confidence intervals)
- Model appropriately for your data type
Complete Example
# Comprehensive analysis example
np.random.seed(42)
data = np.random.normal(100, 15, 200)
# 1. Summary statistics
print("=== SUMMARY STATISTICS ===")
print(f"Sample size: {len(data)}")
print(f"Mean: {np.mean(data):.2f}")
print(f"Median: {np.median(data):.2f}")
print(f"Std Dev: {np.std(data, ddof=1):.2f}")
print(f"IQR: {np.percentile(data, 75) - np.percentile(data, 25):.2f}")
print(f"Range: [{np.min(data):.2f}, {np.max(data):.2f}]")
# 2. Bootstrap confidence interval
n_boot = 1000
boot_means = [np.mean(np.random.choice(data, len(data), replace=True))
for _ in range(n_boot)]
ci = np.percentile(boot_means, [2.5, 97.5])
print(f"\n=== UNCERTAINTY ===")
print(f"Standard Error: {np.std(data, ddof=1)/np.sqrt(len(data)):.2f}")
print(f"95% CI: ({ci[0]:.2f}, {ci[1]:.2f})")
print(f"CI Width: {ci[1] - ci[0]:.2f}")=== SUMMARY STATISTICS ===
Sample size: 200
Mean: 99.39
Median: 99.94
Std Dev: 13.97
IQR: 18.09
Range: [60.70, 140.80]
=== UNCERTAINTY ===
Standard Error: 0.99
95% CI: (97.36, 101.36)
CI Width: 4.00Complete Example (continued)
# 3. Comprehensive visualization
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
# Histogram
axes[0, 0].hist(data, bins=30, edgecolor='black', alpha=0.7, color='steelblue')
axes[0, 0].axvline(np.mean(data), color='red', linestyle='--', label='Mean')
axes[0, 0].axvline(np.median(data), color='green', linestyle='--', label='Median')
axes[0, 0].set_title('Histogram', fontsize=12)
axes[0, 0].set_xlabel('Value')
axes[0, 0].set_ylabel('Frequency')
axes[0, 0].legend()
# Boxplot
axes[0, 1].boxplot(data, vert=True)
axes[0, 1].set_title('Boxplot', fontsize=12)
axes[0, 1].set_ylabel('Value')
axes[0, 1].grid(alpha=0.3, axis='y')
# Q-Q Plot
standardized = (data - np.mean(data)) / np.std(data, ddof=1)
standardized = np.sort(standardized)
n = len(standardized)
theoretical = np.array([np.percentile(np.random.standard_normal(10000),
100 * (i - 0.5) / n) for i in range(1, n + 1)])
axes[1, 0].scatter(theoretical, standardized, alpha=0.4, s=20)
axes[1, 0].plot([-3, 3], [-3, 3], 'r--', linewidth=2)
axes[1, 0].set_xlabel('Theoretical Quantiles')
axes[1, 0].set_ylabel('Sample Quantiles')
axes[1, 0].set_title('Q-Q Plot', fontsize=12)
axes[1, 0].grid(alpha=0.3)
# Bootstrap distribution
axes[1, 1].hist(boot_means, bins=30, edgecolor='black', alpha=0.7, color='lightgreen')
axes[1, 1].axvline(ci[0], color='r', linestyle='--', linewidth=2, label='95% CI')
axes[1, 1].axvline(ci[1], color='r', linestyle='--', linewidth=2)
axes[1, 1].set_title('Bootstrap Distribution', fontsize=12)
axes[1, 1].set_xlabel('Bootstrap Mean')
axes[1, 1].legend()
plt.tight_layout()
plt.show()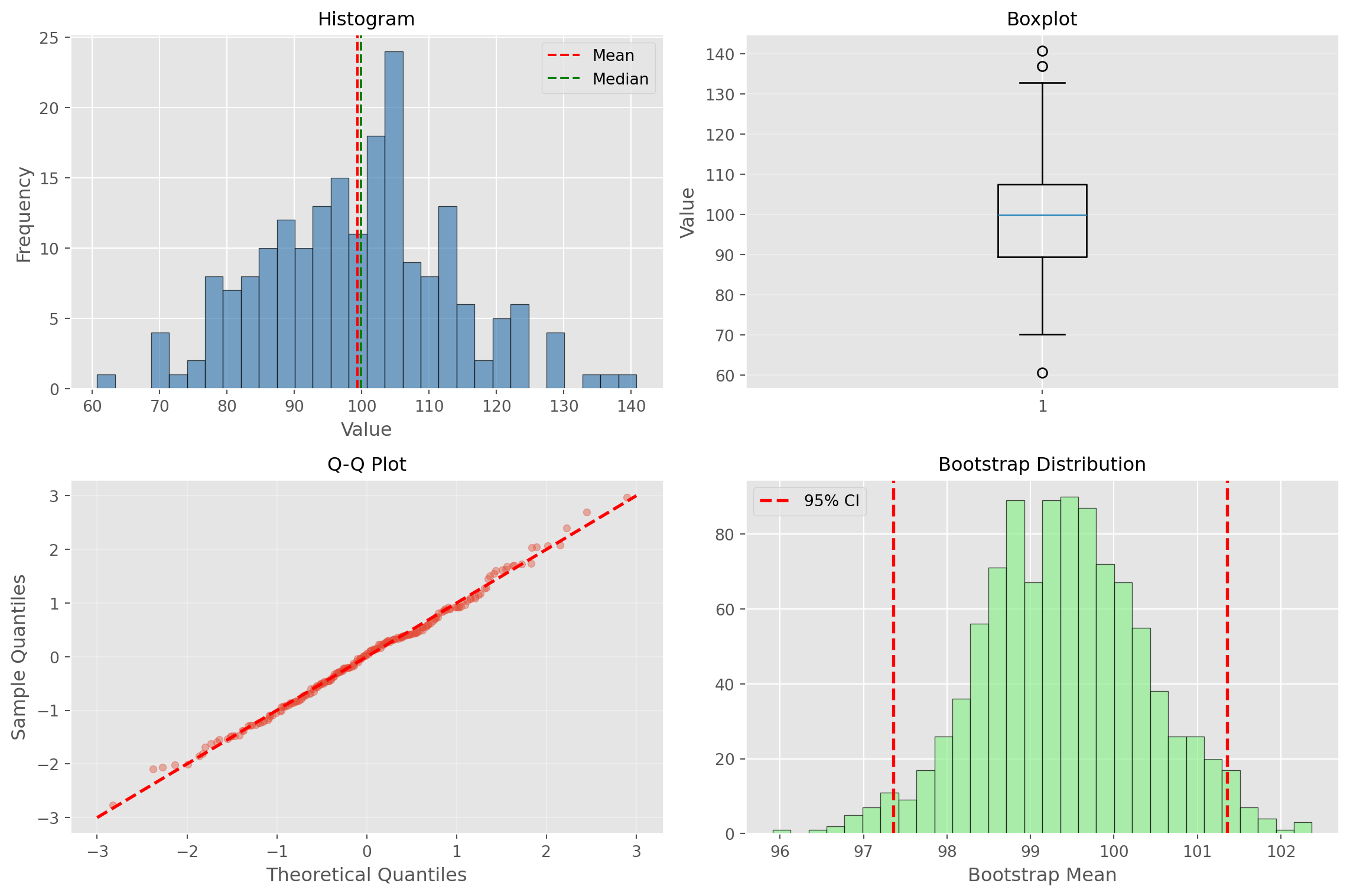
Resources
Python Libraries
numpy: Numerical computingpandas: Data manipulationscipy.stats: Statistical functionsmatplotlib: Visualizationseaborn: Statistical visualization
Further Reading
- Practical Statistics for Data Scientists (Bruce & Bruce)
- Python for Data Analysis (McKinney)
- Statistical Inference via Data Science (Ismay & Kim)
Thank You!
Questions?
Remember:
- Start with exploration
- Quantify uncertainty
- Use appropriate methods
- Visualize your results